Posted 

OpenPano: How to write a Panorama Stitcher

This is a summary of the algorithms I used to write OpenPano: an open source panorama stitcher. You can find the source code on github.

SIFT Feature

Lowe's SIFT [1] algorithm is implemented in feature/. The procedure of the algorithm and some results are briefly described in this section.

Scale Space & DOG Space

A Scale Space consisting of grey-scale images is built at the beginning. The original image is resized in different sizes (AKA. octaves), and each is then Gaussian-blurred by different . Since features are then detected on different resized version of the original image, features will then have scale-invariant properties.

The gaussian blur here is implemented by applying two 1-D convolutions, rather than a 2-D convolution. This speeds up the computation significantly.

In each octave, calculate the differences of every two adjacent blurred images, to build a Difference-of-Gaussian space. DOG Space consists of grey images.

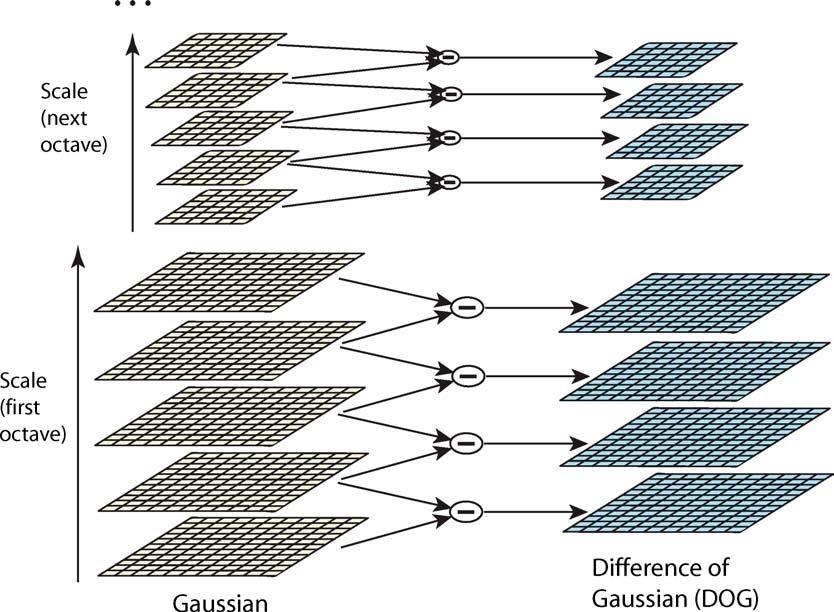
Extrema Detection

In DOG Space, detect all the minimum and maximum by comparing a pixel with its 26 neighbors in three directions: .

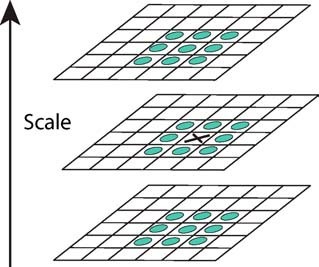
Then use parabolic interpolation to look for the accurate location of the extrema. Reject the points with low contrast (by thresholding pixel value in DOG image) or on the edge (by thresholding principle curvature), to get more distinctive features. The results are like this:

Orientation Assignment

First, we calculate gradient and orientation for every point in the Scale space. For each keypoint detected by the previous procedure, the orientations of its neighbor points will be collected and used to build an orientation histogram, weighted by the magnitude of their gradients, together with a gaussian kernel centered at the keypoint. The peak in the histogram is chosen to be the major orientation of the keypoint, as shown by the arrows below:

Descriptor Representation

Lowe suggested [1] choosing 16 points around the keypoint, to build orientation histograms for each point and concatenate them as SIFT feature. Each histogram uses 8 different bins ranging from 0 to 360 degree. Therefore the result feature is a 128-dimensional floating point vector. Since the major orientation of the keypoint is known, by using relative orientation to the major one, this feature is rotation-invariant.

Also, I followed the suggestions from [2] to use RootSIFT, which is a simple modification on SIFT, and is considered more robust.

Feature Matching

Euclidean distance of the 128-dimensional descriptor is the distance measure for feature matching between two images. A match is considered not convincing and therefore rejected, if the distances from a point to its closest neighbor and second-closest neighbor are similar. A result of matching is shown:

Feature matching turned out to be the most time-consuming step. So I use FLANN library to query 2-nearest-neighbor among feature vectors. To calculate Euclidean distance of two vectors, Intel SSE intrinsics are used to speed up.

Transformation Estimation

Estimate from Match

It's well known [3] that for any two images taken from a camera at some fixed point, the homogeneous coordinates of matching points can be related by a homography matrix , such that for a pair of corresponding point , we have The homography matrix is a 3x3 matrix up to a scale ambiguity. It has the following two possible formulation:

Homography I:

Homography II: with constraint

When two images are taken with only camera translation and rotation aligned with the image plane (no perspective skew), then they can be related by an affine matrix of the form:

Given a set of matches, a matrix of any of the above formulations can be estimated via Direct Linear Transform. These estimation methods are implemented in lib/imgproc.cc. See [3] for details.

However these methods are not robust to noise. In practice, due to the existence of false matches, RANSAC (Random Sample Consensus) algorithm [4] is used to estimate a transformation matrix from noisy data. In every RANSAC iteration, several matched pairs of points are randomly chosen to produce a best-fit transformation matrix, and the pairs which agree with the matrix are taken as inliers. After a number of iterations, the transform that has most number of inliers are taken as the final result. It's implemented in stitch/transform_estimate.cc.

Match Validation

After each matrix estimation, I performed a health check to the matrix, to avoid malformed transformation estimated from false matches. This includes two checks: (see stitch/homography.hh)

  • The skew factor in homography () cannot be too large. Their absolute values are usually less than 0.002.

  • Flipping cannot happen in image stitching. A homography is rejected if it flips either or coordinate.

In unconstrained stitching, it's necessary to decide whether two images match or not. The number of inliers estimated above could be one criteria. However, for high-resolution images, it's common that you'll actually find false matches with a considerable number of inliers, as long as enough RANSAC iterations are performed. To solve this, note that false matches are usually more randomly distributed spatially, geometry constraints of matching can also help filter out bad matches. Therefore, after RANSAC finished and returned a set of inliers, some overlapping test can be used to further validate the matching, as suggested by [5].

Specifically, with a candidate transformation matrix, I could find out the region within one image covered by another image, by calculating the convex hull of the transformed corners. Two filters can then be applied after the overlapping region is found:

  • The overlapping area within two images shouldn't differ too much.
  • Within the region, a reasonably large portion of matches should be inliers. I also used the inlier ratio as the confidence score of this match.

Since false matches are likely to be random and irregular, this technique help filter out false matches with irregular geometry.

Cylindrical Panorama

Necessity of Projection

If a single-direction rotational input is given, as most panoramas are built, using planar homography leads to vertical distortion, as following:

This is because a panorama is essentially an image taken with a cylindrical or spherical lens, not a planar lens any more. Under this setting, the white circle on the grass around the camera (as in the above picture) is expected to become a straight line. A good demo revealing the reason of this projection can be seen at this page.

The way to handle this problem is to warp images by a cylindrical or spherical projection, before or after transform estimation. These are the two modes used in this system. In this section we will introduce the pipeline based on pre-warping, which is used in cylinder mode. This pipeline is generally good, although it has more assumptions on the data and requires some tricks to work well. It is implemented in stitch/cylstitcher.cc.

Warp

We can project the image to a cylinder surface at the beginning of stitching, by the following formula: where is the focal length of the camera, and is the center of image. See stitch/warp.cc. Some example images after warping are given below. Note that this requires focal length to be known ahead of time, otherwise it won't produce a good warping result.

After projecting all images to the same cylinder surface, images can be simply stitched together by estimating pairwise affine transformation, and accumulating them with respect to an arbitrarily chosen identity image. Note that the white line on the ground is more straightened.

Straightening

The cylinder projection equations described above assumes horizontal cameras (i.e. only 1 DOF is allowed for the relative rotation between cameras). This assumption could lead to distortion, then the output panorama would be bended:

Choosing the middle image as the identity help with this problem. Another method I found to effectively reduce the effect is to searching for in the warping formula.

Since the effect is caused by camera tilt, could differ from . The algorithm works by changing by bisection, and find a value which leads to a most straight result. After this process, the result is like:

The change of alone is still not enough, since we are still warping images to a vertical cylinder. If all camera shares a tilt angle, the actual projection surface should be a cone. The error can be seen at the left and right image boundary above. To account for this error, the final trick I used is a perspective transform to align the left and right boundary:

Camera Estimation Mode

Intuition

Cylinder mode assumes a known focal length and requires all cameras to have the same "up" vector, to warp them on cylinder surface at the beginning. We want to get rid of these assumptions.

However, if you simply estimate pairwise homographies, directly stitch them together, and perform a cylindrical warp after the transformation (instead of before), you'll get something like this:

Notice that images indeed are well stitched together: matched points are overlapped very well. But the overall geometry structure is broken.

This is because is inconsistent with the true geometric constraints, as the estimated is unlikely to be of the form . In other words, we estimated as a 3 by 3 matrix up to a scale ambiguity, but not all matrix in is a valid transformation matrix, although they might still match the points. Or to say, it's necessary that the transformation follows the formulation of , but not sufficient.

Also, we noticed that is not a minimal parameterization: assume all adjacent image pairs, as well as the (first,last) image pair are used to estimate homography matrix . Then we are estimating parameters. However, each camera has 3 extrinsic parameters (for rotation) and 1 intrinsic parameter (the focal length). The total degree of freedom would be . If all cameras have the same focal length the total DOF is even smaller.

This inconsistent over-parameterization of camera parameters can lead to the kind of overfitting results above, that breaks the underlying geometry structure.

People use to begin with, because the estimation is just easy linear algebra. But to get true estimation of , of all cameras, gradient-based non-linear iterative optimization are necessary. In geometry vision it's called bundle adjustment, which is simply an initial estimation followed by iterative LM updates.

Initial Estimation

[6] gives a method to roughly estimate the focal length of all images at first. Given all focal length and the rotation matrix of one image, the rotation matrix of a connecting image can be estimated by using the homography we already have:

Therefore, the estimation procedure goes like a max-spanning tree algorithm: after building a pairwise-matching graph, I first choose an image with good connection property to be identity. Then, in each step a best matching image (in terms of matching confidence) not processed yet is chosen and its rotation matrix can then be roughly estimated. Based on the rough estimation, all cameras added so far are then globally refined by bundle adjustment to be explained in the next section. This procedure is implemented in stitch/camera_estimate.cc.

Note that, since the homography is an inconsistent parameterization, the result calculated from the above equation might not be a proper rotation matrix. Therefore I actually used the closest rotation matrix in terms of the Forbenius norm. Formally speaking, given , we compute:

If no bundle adjusment is performed, the stitching result will misalign and looks like this, due to wrong formulation of and errors in estimating :

To further refine the parameters in and such that matched points are aligned properly, optimization over the consistent parameterization is needed.

Bundle Adjustment

We setup a consistent parameterization of and in the following ways: Here, is the angle-axis parameterization of rotation matrix. Let be a vector of all parameters in the system. We aim to minimize the reprojection error of all matched point pairs: where is the 2D projection of point in image to image , under and : . The above sum is over all pairwise point matches found among all images added to the bundle adjuster so far. Note that when stitching an unordered collection of photos, one image can match a number of others. These matches all contribute to the bundle adjuster and help improve the quality.

Iterative methods such as Newton's method, gradient descent, and Levenberg-Marquardt algorithm can be used to solve the optimization. Assume matrix , where is the vector of all residual terms in the sum of square optimization: , then the three optimization methods can be formalized as follows:

  • Gradient descent:
  • Newton's method:
  • LM algorithm: , where is diagonal.

All iterative methods involve calculating the matrix . It could be done numerically or symbolically.

  • Numeric: For each parameter , mutate it by and calculate respectively. Then

  • Symbolic: Calculate by chain rule. For example, some relevant formula are:

The last equation is from the result of [7]. By the way, it's interesting to point out that Lowe's paper [5] actually gives an incorrect formula: This doesn't hold because the notation is not element-wise exponential, but matrix exponential.

Both methods are implemented in stitch/incremental_bundle_adjuster.cc. Symbolic method is faster because it allows us to calculate only those non-zero elements in the very-sparse matrix , and also allows us to calculate as well as together in one pass, without the need to do large matrix multiplication.

In a collection of images, optimization will be run times, when each image is added. Each optimization ended when the error doesn't decrease in the last 5 iterations.

After optimization, the above panorama looks much better:

Straightening

Straightening is necessary as well. As suggested by [5], the result of bundle adjustment can still have wavy effect, due to the tilt angle ambiguity. By assuming all cameras have their vectors lying on the same plane (which is reasonable), we can estimate a vector perpendicular to that plane to account for the tilt and fix the wavy effect.

See the following two images and notice the straight line on the grass is corrected (it is actually a circle in the center of a soccer field).

Blending

The size of the final result is determined after having all the transformations. And the pixel value in the result image is calculated by an inverse transformation and bilinear interpolation with nearby pixels, in order to reduce alias effect.

For overlapped regions, the distance from the overlapped pixel to each image center is used to calculate a weighted sum of the pixel value. I only used the distance along the axis to calculate the weight, to get better result in panoramic image. The result is almost seamless (see images above).

Cropping

When the option CROP is given, the program manages to find the largest valid rectangular within the original result.

An algorithm is used, where are the height and width of the original result. The algorithm works like this:

For each row , the update for every can be done in amortized time, and the maximum possible area for the first rows, would be .

BTW, you can download these papers with my automatic paper downloader:

pip install --user sopaper
while read -r p
do
  sopaper "$p"
done <<EOM
Distinctive Image Features From Scale-invariant Keypoints
Three Things Everyone Should Know to Improve Object Retrieval
Random Sample Consensus: a Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography
Automatic Panoramic Image Stitching Using Invariant Features
Construction of Panoramic Image Mosaics with Global and Local Alignment
A Compact Formula for the Derivative of a 3-D Rotation in Exponential Coordinates
EOM
#

Comments

×